Random forest is one of the widely used machine learning models for supervised learning task. It is robust to missing values in dataset as well as to outliers. It is an ensemble of many decision trees. Therefore, it achieves good accuracy in practice. In this post, I will present detail mathematics of how a Random forest works.

Supervised learning can be divided into Classification and Regression.

• Classification is supervised learning where target variable is categorical
• Regression is supervised learning where target variable is numeric

Dataset

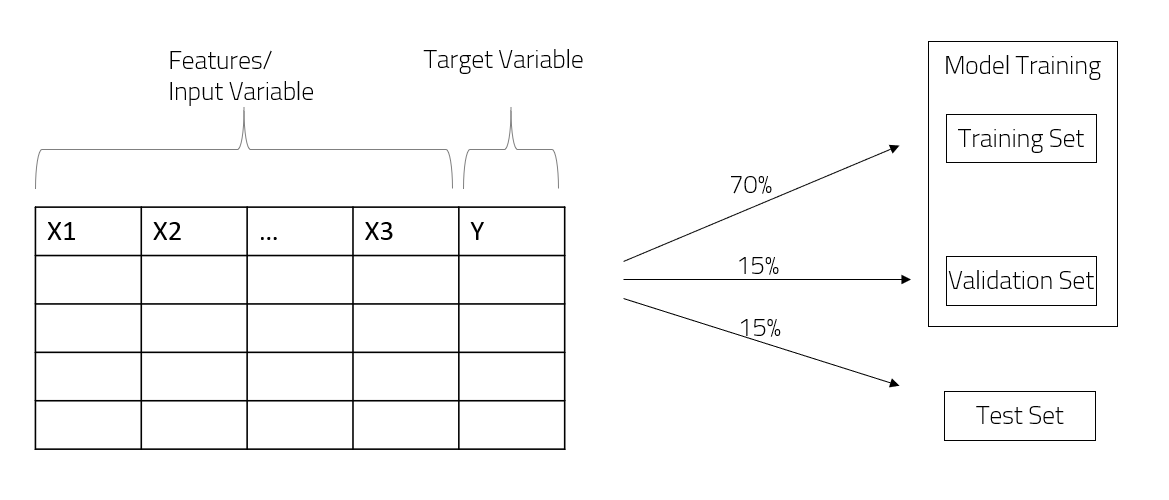
A model is trained to learn relation mapping between a set of input features and target feature on a given dataset. Hyperparameters define various characteristics of the model ranging from complexity, learning rate of the model. These are set by taking best performance measured on the validation dataset. Model’s final performance is reported on the test dataset.

Classification

A toy classification task will be used to present the material. Given color and diameters of different fruits, classification task is to determine exact fruit label: grape, lemon, apple. 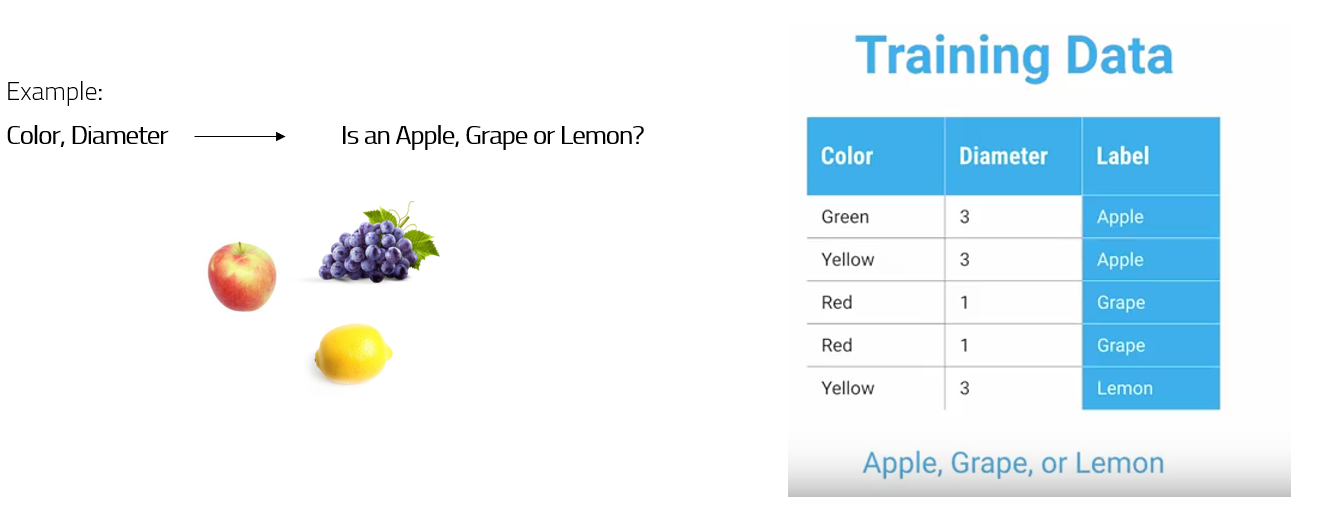Image courtesy: https://www.youtube.com/watch?v=LDRbO9a6XPU&t=85s

I will explain how a decision tree can be used to perform classification. Decision is also the building block of Random forest. Decision tree progressively asks questions with binary (Yes/No) answers. 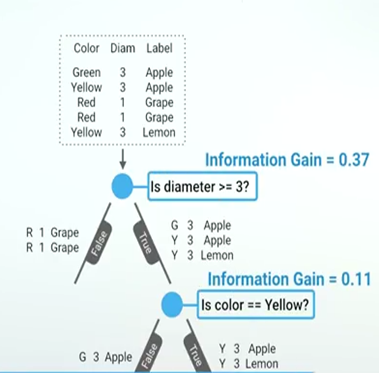Image courtesy: https://www.youtube.com/watch?v=LDRbO9a6XPU&t=85s

Records for which answer is No are separated into a (left) group and records with answers Yes are separated into another (right) group. Process of grouping records continues untill one of the following:

• One record left in a group
• Group does not have any mixed labels. For example, all fruits are grapes
• There is no question left that can separate records into two groups by unmixing label.

By now you may have realized that the goal is to separate records with mixed lables so that in sub groups there are as little mixing in labels as possible. Mixing of labels are measured using Gini impurity and Entropy. I will explain Gini impurity. However, Entropy also works in a similar fashion.

Gini impurity (GI)

GI measures how mixed the labels are. It is 0 when all records have the same label and the highest when all records have distinct labels. GI of the dataset is calculated in the following. Let it be denoted by GI_parent-node

GI of the sub groups can also be measured. Let the summation of the GI of the subgroups be denoted by GI_split Impurity of the subgroups can be measured in the following way.

Reduction in impurity as a result of separating records is the information gain.

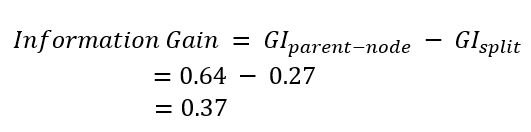
Inference

Once the tree is build, it can be used to label a record. Based on different attributes’ value of the record, one path is followed in the tree. Majority of the labels at the leaf node determines the final output of the record.
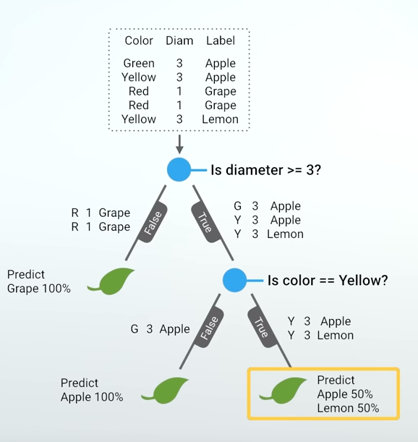Image courtesy: https://www.youtube.com/watch?v=LDRbO9a6XPU&t=85s

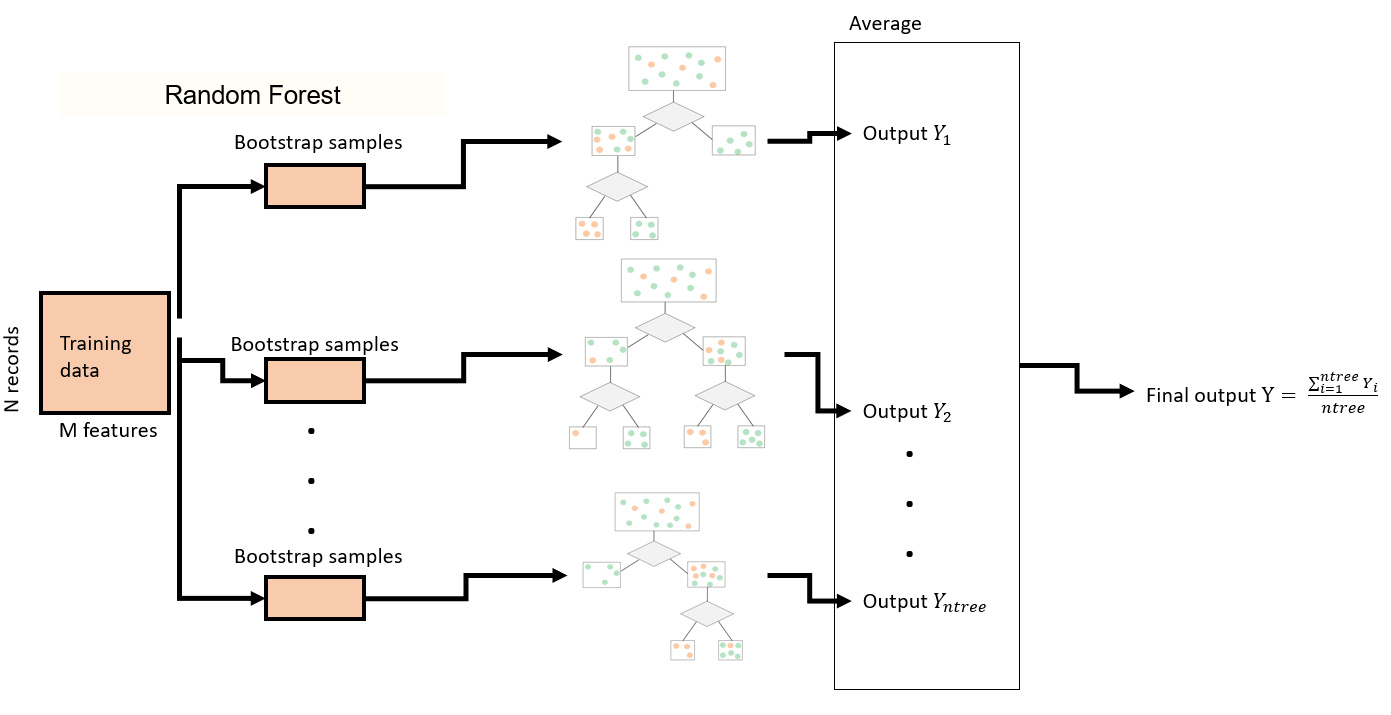
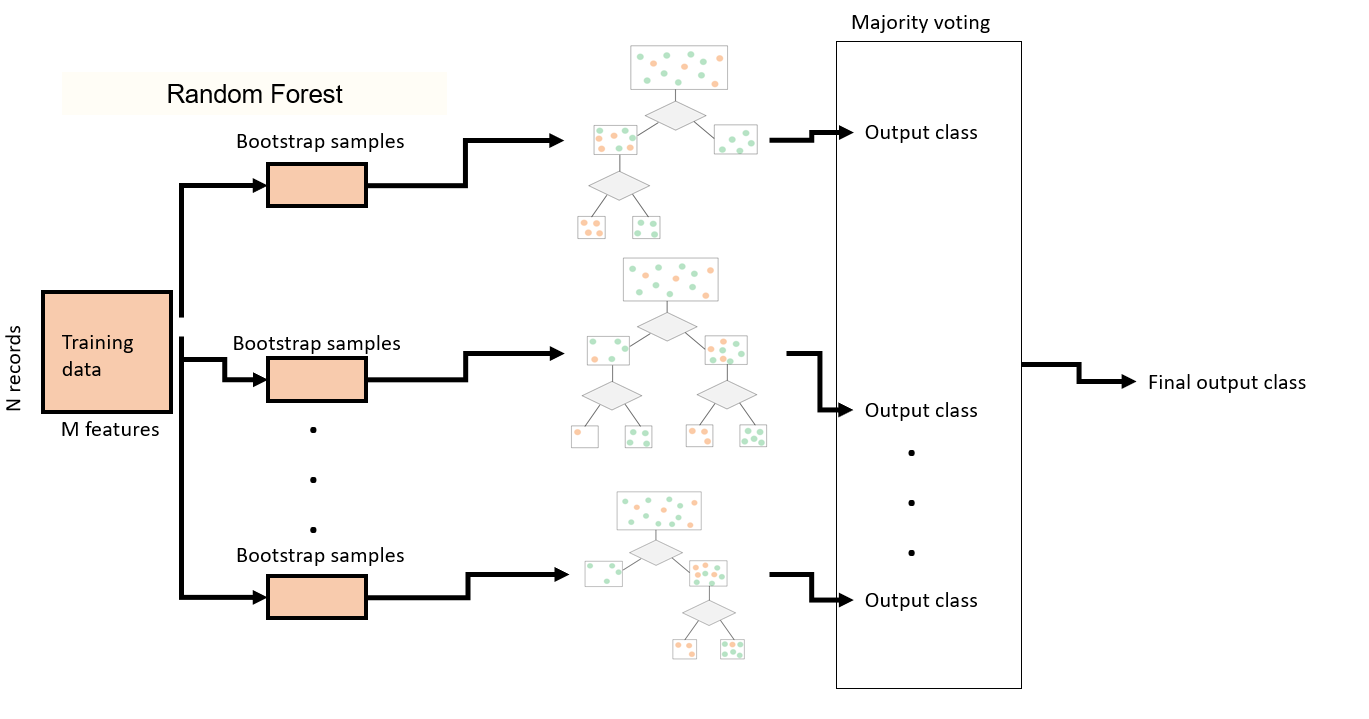
Ensemble of trees: Random Forest

A Random forest is a collection of trees that are grown independent of each other by taking random subsamples of records and features. Inference is done by taking a majority vote among the trees.

Feature importance

Defines how much impurity a feature reduces in the forest

• Sum of reduction of Gini impurity when a feature is used to split a node in a tree
• Calculate weighted reduction by using the number of records reaching the node
• Take average over all the trees
• Normalize the scores across features from 0 to 100 to produce a relative ranking among features

Regression

Regress is supervised learning where target variable is numeric. For example, predicting house price is a regression problem.

Goals in Regression are the following:

• Reduction in variance in target variable Y
• Variance defines how scattered Y is
• Applies Mean squared error (MSE) with mean as output value (𝑌)
• Given s is a cut-point for a feature f
  
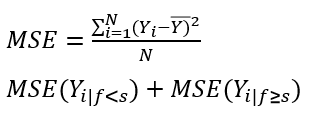
  Example:
  
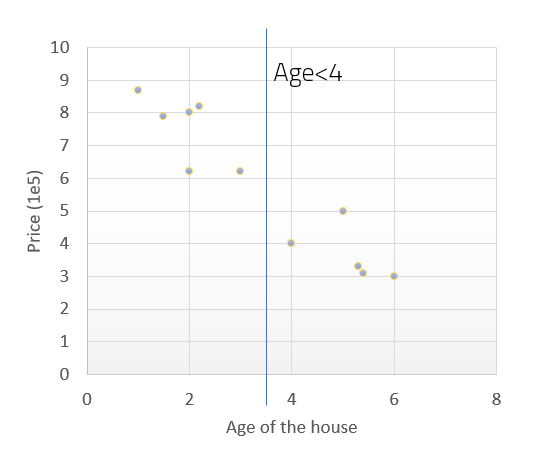
• Random forest performs average of the individual predictions.