Training a neural network may take days or weeks. A faster training method will save researcher and practitioner’s time. There are various methods to train a neural network in a distributed manner. These methods distribute the Stochastic Gradient Descent (SGD) optimization over multiple compute nodes. These methods are outlined here:

1. Parameter server method
2. Parallel Allreduce method
3. Ring Allreduce method

[1] Parameter server method:
There is a central node that acts a server storing gradients from all compute nodes. Each compute node get a set of minibatches of data. Once they compute gradient on their local minibatch, the gradient is sent to the parameter server. The server then aggregates all the gradients and send the aggregated copy to each compute node to update the model weights. Failure of the parameter server can be a bottleneck for this approach.

[2] Parallel Allreduce method:
There is no central parameter server in this method. Each compute node calculates gradient on its own minibatch of data and then sends its gradient to every other nodes. Once it starts receives gradients from all nodes, it aggregates the gradients and use them to update the weights of the neural network before starting computation for the next iteration of SGD. This approach works well when there is very reliable and fast communication available among compute nodes. If there is a slow compute node or slow network can be become a bottleneck.

[3] Ring Allreduce method:
In this method, compute node uses both upload and download bandwidth during communication. Compute nodes are organized in a ring where a node has an incoming connection to a neighbor and an outgoing connection to another neighbor. When a node finishes computing gradients on its minibatch, it sends the gradient to its neighbor. In the same round, the node also receives gradient from its incoming connection. Each node has a buffer where it stores gradients from all nodes in the ring. When there are \(K\) nodes in the ring, it takes \((K-1)\) rounds of communication for a node to receive gradients from all the nodes in the ring. A slow compute node can reduce efficiency of this method since all the other nodes need to wait for its gradient. 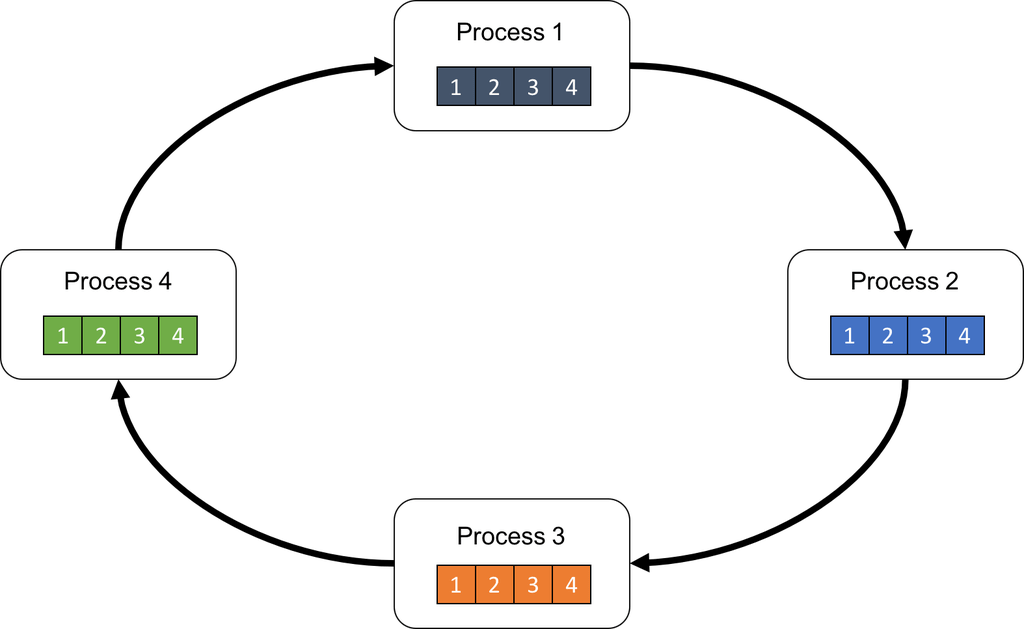Conceptual diagram of ring allreduce method (https://preferredresearch.jp/2018/07/10/technologies-behind-distributed-deep-learning-allreduce/)

DeepSpeed implements several smart techniques to train a large scale deep learning model. It features:

• 1bit-Adam: It begins with a warmup stage, which is the vanilla Adam algorithm; followed by the compression stage, which keeps the variance term constant and compresses the linear term momentum in 1-bit representation.

• Zero: Optimizations to reduce memory redundancy in parallel training devices, by partitioning weights, activations, and optimizer state.

• Sparse attention: It can compute local attention between nearby tokens, or global attention via summary tokens computed with local attention. It can also allow random attention or any combination of local, global, and random attention

• Data, Model and pipeline parallelism all at the same time

Some best practice to follow in distributed training

• Each rank / parallel process can generate their own log and tensorflow warnings. It may result into huge standard out log. All the ranks’ output except for rank 0 can be redirected to file. Below is an example with Horovod:

  if hvd.rank() > 0:
    outfile = open(os.path.join(FLAGS.train_dir, f"rank{hvd.rank()}.stdout"), "w")
    sys.stdout = outfile
    sys.stderr = outfile
  

Latest research works

Delay compensated Asynchronous Stochastic Gradient Descent

Zheng, Shuxin, et al. "Asynchronous stochastic gradient descent with delay compensation." Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.

• Setup involves a parameter server and many workers as outlined in the figure

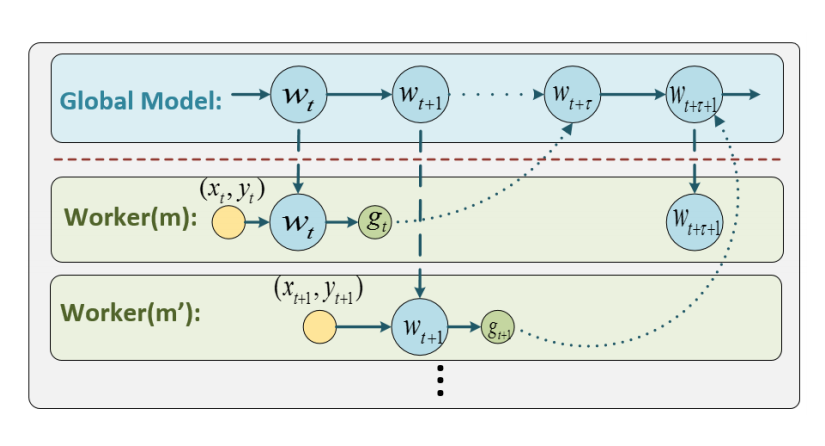
• Workers receive a chunk of the training dataset and compute gradient on them. They send the computed gradient to the parameter serve

• Parameter server who maintains the global gradient by aggregating gradients from all the worker nodes. However, it does not wait for all the workers to finish their iteration. When a worker node sends its gradient, the server updates the weights and send the weights to the worker that just communicated. The worker then can start the next iteration of gradient computation.

• Asynchonous setting runs into problem when there are slow workers. Gradient sent by a slow worker can lag by few iterations than weights that are stored at the server.

• Model update in ASGD is equivalent to Taylor series expansion of 0th term. It ignores higher order terms which corresponds to update using stale gradients from slow workers. We can consider to include one additional term from the Taylor series which would be a derivative of the gradient, in other words Hessian matrix. However, computing Hessian matrix is computationally expensive. So it is approaximated by element-wise multiplication of the stale gradient with itself weighted by a scalar lambda times the difference between fresh model and stale model. It is given by the following equation. For proof, please refer to the paper:
  

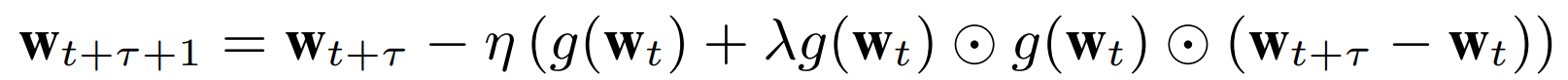
• Delay compensation technique allows a server to store a backup of each worker weights. When a worker sends its gradient, it corrects the gradient based on an approximate Hessian matrix as well as considering the difference between the fresh weights of the parameter server and the possibly stale weights of the worker by using the backup.

• Vanilla ASGD consider 0th term in the Taylor Series Expansion to approaximate a fresh gradient of the parameter server at a given time step. Vanilla ASGD ignores all the higher order term in the expansion series. If it considers the higher order term during the update, the optimization will converge. However, applying higher order term of the Taylor series is computation intensive.

• It is possible to show that element wise product of gradients becomes close to the Hessian matrix when iteration number t approaches infinity. Intuitively, after training for sufficient epoch or iteration, a neural network can approaximate any function. Let denote lambda * g(t) DOT g(t) as the term to approaximate the Hessian matrix.

• When the parameter server updates the global gradient by adding the stale gradient from the slow worker, it approximates the slow worker’s gradient as if it were fresh. The approximation is the correction. It replaces stale g(t) by g(t) + lambda * g(t) DOT g(t) DOT (w(t+p)-w(t)) where w(t+p) is the fresh weight of the parameter server and w(t) the last fresh update of the slowest worker from the backup stored at the parameter server.

• Zheng et al. show the delay compensated method performs close to Synchonous SGD on ImageNet dataset

Stochastic Gradient Push (SGP)

Assran, Mahmoud, et al. "Stochastic gradient push for distributed deep learning." arXiv preprint arXiv:1811.10792 (2018).

Distributed Stochastic Gradient Descent Algorithm to train neural network faster. They overlap communication with computation to avoid communication bottle neck. Their work is faster than ALLREDUCE where each worker communicates with every other worker. In a setting where communication is a bottleneck, allreduce approach is not feasible. Parameter server is asynchronous but poses a single source of failure risk. Push sum SGD have been benched marked against existing distributed training method which show it achieves similar accuracy on validation set but on a significantly less time. A simple summary of the SGP algorithm is given below

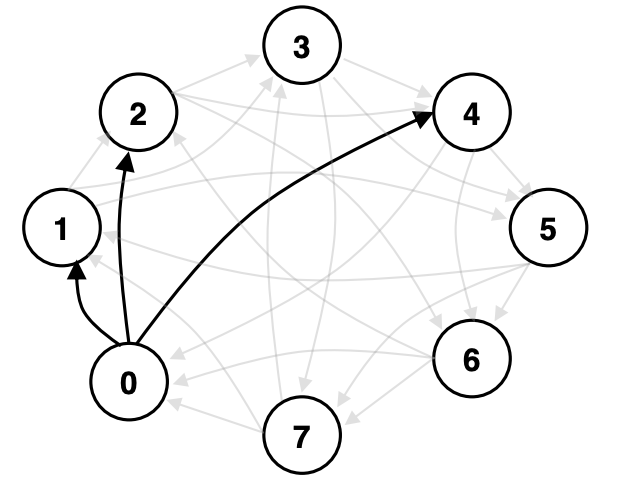
Directed communication graph denoting node 0’s neighbors [Assran et al. 2019]

• SGP maintains a communication mixing matrix that determines which compute node communicates with what other nodes. It is a weighted adjacency matrix. In a parallel SGD, each entry is \(\frac{1}{n}\). In SGP, each node choose its own weights for its neighbors independent of other nodes in a given iteration. When a node sends its parameters to a neighbor, it also sends the communication weight along with the parameter values. The neighbor, upon receiving, add the weighted parameter value to its own value.
  Idea of mixing weight matrix denotes communication topology among nodes. From Markov Chain literature, it can be shown that after doing some rounds of communication, a gradient from each node eventually reaches every other node despite missing direct communication link.

[Assran et al. 2019]

• Asymmetric communication happens where a node sends to another node but not necessarily needs to receive gradient from that node. To overcome challenges associated to designing an algorithm ensuring \(\pi = \frac{1}{n}\), authors introduce another scalar \(w\) which is initially set to 1 and eventually becomes same as the number of nodes. Each node updates their gradient by further normalizing with the weighted \(w\) for a given iteration.

• SGP also proposes to perform local gradient update for \(\tau\) iteration where \(\tau\) is bounded. Typically, SGD can converges even when gradients of individual nodes are outdated by one or two iterations. If a node is passed \(\tau\) iterations but still has not received gradients from all of its neighbors, then it enters a blocking mode and waits for the remaining gradients from its neighbors. Upon receiving the gradients, the node update its parameters in line 6-8 of the SGP algorithm. Then it proceeds by updating model weights in line 3-4.